Let's Learn x86-64 Assembly! Part 3 - Arithmetic and Logic
published on Dec 30 2020

This post is a part of a series on x86-64 assembly programming that I'm writing. Check out parts 0, 1 and 2! .
The header image shows a chunk of the arithmetic-logic unit (ALU) from 8086 - the ancient predecessor of modern-day Intel processors. The image is a part of a microscopic photo of the processor die made by Ken Shirriff.
Well, I'm finally bringing this series back from a months-long hiatus! In the last post, we started implementing an emulator for a simple instruction set of our own. We sketched out the overall architecture, and implemented a few instructions for moving data between virtual registers and memory, learning about the corresponding x86-64 instructions along the way. In this one, I want to focus on arithmetic and logic operations, which will allow our emulator to do stuff that is a bit more interesting than just moving bytes around. But before we jump into that, I want to briefly talk about how numbers are represented in a computer.
Number Representation
If you've made it this far in the tutorial, chances are that you understand the basics of how the binary notation for numbers works, and don't need an explanation of what bits and bytes are. So I'm not going to spend time on that.
However, there are some particular details related to representing signed integers. Theoretically, this topic should be a part of any computer science curriculum. But not every coder has a formal CS background, and even among those that do, most either don't remember or have never encountered these things in practice - because one simply doesn't have to think about them for the vast majority of time when programming computers.
But number representation is important for understanding the arithmetic instructions that we're going to be looking at; therefore, I feel like I can't simply gloss over the topic.
If you already know how signed integers work in most computers, this might be a good refresher, otherwise you might learn something new!
Representing Integers
Computers can't represent "numbers" in the abstract, mathematical sense. They're finite, discrete machines and there's not enough memory in the world to store a representation of an arbitrarily large quanitity, or even the representation of a rather small, but "weird" quantity like tau.
We cope with that limitation by conceding that we'll never be able to represent an arbitrary number. Instead, we use the resources at our disposal to represent a subset of all numbers. We look at all the bit strings of a fixed length, and agree that each of them represents a particular number. However many different bit strings we can deal with, that's how many different numbers we can represent.
For example, we can represent 256 distinct numbers using 8 bits, because there are 256 different bit strings of length 8. Generally speaking, it is entirely up to our interpretation which 256 numbers these strings represent. For example, you could decide to interpret each of the 8 bits as a binary digit, so that the entire 8-bit bitstring is nothing more than its corresponding number, written out using the binary numeral system. On the other hand, you might decide that the first 6 bits specify the "whole" part of the number, and the remaining 2 bits specify the "fractional" part (this is called fixed-point representation and used to be commonplace before the wide spread of hardware-accelerated floating point arithmetic). It all depends on which subset of numbers interests you at any given moment.
Certain instructions of a given processor have baked-in assumptions about the representation used by their parameters, and behave accordingly. For example, the addps SSE instruction assumes that its parameters are floating point numbers adhering to the IEEE 754 standard. We're more interested in instructions doing simple integer arithmetic, but those also assume a certain representation, as we're about to see.
Let's have a look at some of the possible ways to represent integers in a computer. For the sake of simplicity and readability, I am going to use eight bits for everything, but all of this extends to a larger number of bits in a straightforward manner.
In case of positive integers, the simple and straightforward mapping is to just use a given integer's binary representation, as we've mentioned before. If the representation doesn't take all of the available eight bits, we'll pad out the number with zeroes from the left (the additional whitespace in the middle of the bit string is added just for readability):
| Decimal number | Binary number | Bit string |
| 0 | 0 | 0000 0000 |
| 1 | 1 | 0000 0001 |
| 2 | 10 | 0000 0010 |
| 3 | 11 | 0000 0011 |
| 4 | 100 | 0000 0100 |
So far, so good. But things start to get sticky when we introduce negative numbers into the mix. How would you represent a number like -5? Sure, if you were doing math with a pencil and a piece of paper, you could just write "-101" instead of "-5" and be done with it, but you can't exactly do that with a computer.
The initial instinct might be to use the leftmost (most significant) bit to indicate the sign. If the very first bit of a bit string is 0, then we assume the number to be positive. If it is 1, we assume the number to be negative. This way of coding signed numbers is called "sign-and-magnitude representation" and it was used in some very old machines.
| Decimal number | Binary number | Bit string |
| -3 | -11 | 1000 0011 |
| -2 | -10 | 1000 0010 |
| -1 | -1 | 1000 0001 |
| 0 | 0 | 0000 0000 |
Astute readers might have noticed an interesting problem here. We've assigned the string "0000 0000" to 0, but how are we to interpret the string 1000 0000? It's -0, so the effective value it represents is just 0. It looks like we ended up with two representations for a zero - one "positive" and one "negative".
While having two representations for the same number is kind of ugly, it's actually the least of our worries. In fact, the standard for floating point, IEEE 754, mentioned earlier, does have the notion of "negative zero", and it's no big deal. But nevertheless, the sign-and-magnitude representation is not used on any modern machine that I am aware of. That is because there is a much better way of representing signed integers, that not only avoids having two representations for 0, but actually ends up being much easier to deal with in hardware. However, in order to really understand why this alternative representation we're about to propose is better, we need to take a little detour.
Learning to Add
Let's mentally put integer representation on the backburner for a minute. Let's think about how CPUs work on the lowest possible level (the lowest that I can grasp myself anyway).
The most basic component of a CPU is a switch that can be controlled by an electrical current: when a current is present, the switch is ON, and when there is no current present, the switch is OFF. You could build a crude switch like that yourself using a few pieces of metal, insulation and some wire - it's called a relay.
Some early machines might have used relays (which were huge and unreliable), but modern machines use a different kind of switch - the transistor, which is semiconductor-based. It's extremely reliable, and can be made so tiny that it's possible to cram billions of these things into a small space. Still, the principle is the same - a transistor is a simple switch, controlled by electrical current, it's just miniscule in size.
By wiring switches together in a particular manner, one can build logic gates - tangible hardware implementations of the AND/OR/NOT/XOR/etc. functions that most programmers are familiar with. For example, here's a diagram showing how you can build an OR logic gate from two switches:
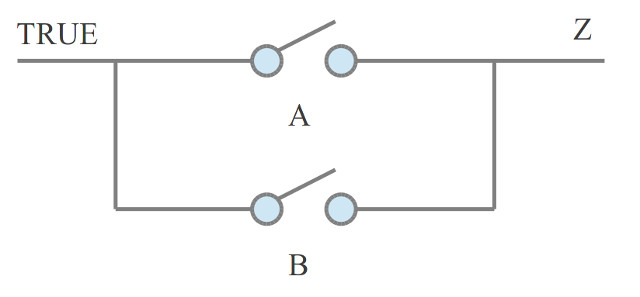
Image credit: simplecpudesign.com
If any one of the switches (labelled A and B respectively) is turned on, the output (labelled Z) will have current. If both A and B are off, Z will have no current. Switches act as "operands" for the logical OR operation, and the output Z represents the result.
Logic gates can be further wired together to make more complex circuits, and so on.
So, fundamentally, a CPU is a giant collection of interconnected logic gates that consist of tiny electrically operated switches. With that in mind, I invite you to consider the question: how does a CPU actually do arithmetic? For example, how does it add two positive integers?
Turns out, you can wire together logic gates to make circuits that can perform arithmetic operations.
Let's consider adding two single-bit numbers. Forget about negative numbers for now, let's just handle positives. Note that result itself can be larger than 1 bit, so we'll add a second, "carryover" bit to it. There are only 4 possibilities:
- 0 + 0 = 0 in the result bit, 0 in the carryover bit
- 0 + 1 = 1 in the result bit, 0 in the carryover bit
- 1 + 0 = 1 in the result bit, 0 in the carryover bit
- 1 + 1 = 0 in the result bit, 1 in the carryover bit
The pattern in the result bits looks like a truth table for a familiar boolean operation - exclusive OR (aka XOR). The pattern in the carryover bit looks like the truth table of a boolean AND operation. So, a circuit for adding two single-bit values can be built with a XOR gate and an AND gate. It's called a half-adder:
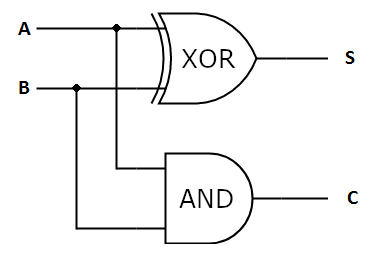
When we try adding two 2-bit numbers, things start to get real hairy. We need to take into account the carryover bit from adding the first two bits when adding the second two bits. So we can't just string together two half-adders to add two 2-bit numbers. We need to design a circuit that adds three bits: two "regular" bits and one carryover bit from the previous single-bit addition. Such a circuit is called a full adder:
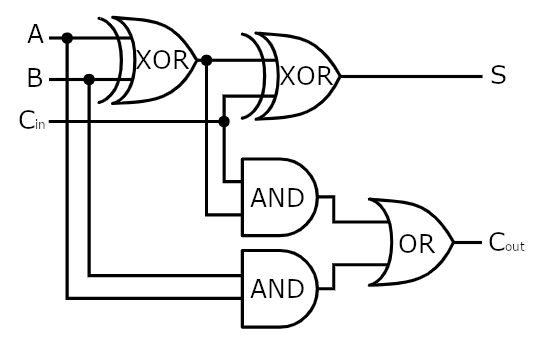
By stringing together a half-adder and a full adder, we can finally get a circuit that can add two-bit numbers:
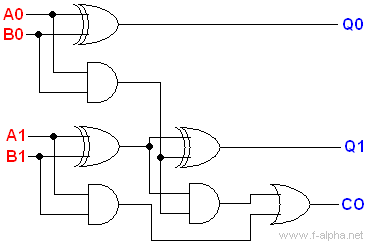
In general, by stringing together several full adders one after another, we can build blocks for adding numbers with more bits. Such blocks are called ripple-carry adders.
It's not actually that important for you to understand what the circuits above are doing in great detail. In fact, a ripple-carry adder is just one of a number of possible designs for adding two numbers, and it's not even necessarily the best. What I hope you'll take away from all of the above is that seemingly simple operations can get surprisingly hairy when implemented in hardware, spawning a mess of logic gates - and hardware doesn't like complexity. Simplicity and compactness is a virtue here - it means less components, less wires, less heat.
This is what motivates an alternative representation for integers - if it means we can afford to build less hardware, then it's better!
Integer Representation Revisited
Now that we got a very small taste of what it's like to actually represent ephemeral logical ideas in real hardware, we can re-evaluate our "sign-and-magnitude" representation of integers from a new perspective. How would we go about designing a circuit for adding two signed integers that use this representation?
For starters, if both integers have the same sign, then we can simply add their unsigned parts using the same type of circuit we've shown above, and then tack the sign onto the result. On the other hand, if the signs are different, we would need to design a new type of circuit, let's call it a "subtractor", to handle that case. There might be some other ways of doing it as well. It's certainly possible to pull off (and some early computers did), but it comes at the cost of additional complexity.
But there's no real need for this complexity. As it turns out, it's possible to just use the ripple-carry adder described above with no modification to do both addition and subtraction. All we have to do is just alter our integer representation!
Two's Complement
Let's think about subtraction for a second. How would we do subtraction with binary numbers if we were to do it "manually"? Let's consider this example:
110
-101
Remembering the method of subtraction they taught us in school, we'd start going through pairs of digits right-to-left. The first pair of digits is 0 and 1. Since 0 is less than 1, we turn that first 0 into a 10 (borrowing 1 from its neighboring digit to the right in the process). 10 - 1 = 1, so we record 1 into the last digit of the result. The next pair of digits is 1 and 0, but since we've borrowed 1 in the previous step, it's actually 0 and 0, so we record 0 - 0 = 0 into the second digit of the result. Next come 1 and 1. Since 1-1 = 0, we record 0 into the first digit of the result, and thus we have the result - 1 (quite expected since 110 comes immediately after 101).
That's cool, but how does it help? Well, since a -N is nothing more than 0 - N, why not look at what happens when we subtract a binary number from 0 using this method?
0000 0000 (0)
-0000 0100 (4)
__________
1111 1100 (-4 ??)
We have something interesting here. Check this out: adding this supposed "-4" to a 5 (modulo 256) in a straightforward manner yields the expected result:
1111 1100 ("-4")
+0000 0101 (5)
__________
0000 0001 (1 !!)
It's also quite obvious that adding 1111 1100 to 0000 0100 modulo 256 will produce a 0, which is exactly what we want. It looks like we've found the representation that we were looking for.
Can we obtain this negation of a binary number in some simple way that can be easily expressed with circuits? If we look at what's happening when we subtract N from 0, we'll observe that all the bits of the result starting from the rightmost one are the same as the bits of N up to and including the first nonzero bit. The bits after that are the inversion of the corresponding bits of N:
0000 0000
-0101 1000
__________
1010 1000
But this is actually the same exact thing as inverting all bits of N and then adding 1 to the result! Why is that? When we invert all bits, the rightmost zero bits will turn into ones. The rightmost nonzero bit - let's say it's in position `i` - will turn to zero. Adding 1 will flip back all the bits from the right up to and including that bit in the i-th position. The bits after the i-th position will remain inverted.
So, to summarize: in our new integer representation, nothing changes for positive integers. To represent a negative integer, we flip the bit representation of its absolute value and add one.
This is called "two's complement", and this is what's used on all modern machines. This representation has the advantage that it Just Works with the same exact logic circuits that are used to add unsigned integers, and we don't even need a separate block for doing subtraction: like in real math, "subtraction" is just addition of a negative number to a positive one. Two's complement also neatly sidesteps the double-zero issue (instead, we get one extra number in the negative range).
And with this, the "theoretical" portion of this post is over. Now let's talk about specifics.
Flags
Before we jump into x86-64 arithmetic and logic instructions, we need to familiarize ourselves with flags. I've already touched on this concept in one of the previous posts. Flags are single-bit values, each of which tells us a "yes or no" fact about the outcome of a previous operation. For example, the "zero flag", or ZF for short, indicates whether the last operation that could have affected the flag, resulted in a 0.
The flags on x86-64 live in a special register called
rflags. You can't read that register directly,
but you can, for example, save its contents to the stack using the
pushfq
instruction. You also can't change that register directly - it is affected
indirectly in specific ways by the instructions being executed by the
processor. Another way to change it indirectly would be to use
popfq.
The flags affect the behavior of control flow instructions (which we will discuss later).
So why do we need to learn about flags now? Because arithmetic and logic instructions affect them. x86-64 has several flags, so we'll list only those that are relevant to us at the moment:
- Overflow Flag (OF) - this flag is set if the result of an operation would not fit into the target number of bits. Integer overflow, by the way, is something that happens more often than you might think, and can cause mysterious bugs. Generally, what happens on int overflow is up to the higher-level language that compiler is emitting code for. In case of C++, unsigned ints wrap around back to 0, and for signed ints the behavior is undefined (not going to get into why here). To mitigate that, you can configure your compiler to trap on int overflow. This is great in debug builds - you can see the problem manifest immediately instead of running full steam ahead with undefined behavior. But, unfortunately, it has a significant runtime cost.
- Sign Flag (SF) - this flag is usually set to the most significant bit of the result. If the result is interpreted as a signed integer, this flag being 1 indicates that the result is negative.
- Zero Flag (ZF) - as already mentioned, set to 1 when the result of the previous operation is 0.
- Carry Flag (CF) - usually this indicates that a carry or a borrow was generated out of the most significant bits when performing addition or subtraction. For example: performing 1111 1111 + 0000 0001 would set the carry flag (when we get to adding the leftmost bits, it will require a carry operation). Performing 0000 0000 - 0000 0001 would also set the carry flag. However, 0111 1111 + 0000 0001 would clear the carry flag.
Note that the descriptions above are what the flags mean usually, but some instructions may set or clear them unconditionally, and some others may leave them undefined. We'll call out such cases explicitly.
There's a lot of flags we're skipping over, but they're either not relevant for the subject of this post or are archaic remnants from the olden days, like the parity flag (consider popcnt instead). Going forward, we'll be dealing with only these flags, and these are the flags QBX will support.
Arithmetic Instructions
Now is the time for us to examine some of the arithmetic and logic instructions of x86-64 and implement their equivalents for QBX.
ADD and SUB
We'll start with good old addition. The add
instruction adds together the source and destination operands, and records the
result into the destination operand. The destination must be either a register,
or some location in memory, while the source can be a register, a location in
memory or an immediate value.
Note, however, that just like with mov, both
operands cannot be memory. Another interesting curiosity is that while you can
mov a 64-bit constant value into
a 64-bit register, you can not directly
add a 64-bit constant to a 64-bit register.
You'd first have to mov it to an another
register. This is the case with practically all x86-64 instructions - I am
fairly confident that mov is the only one that
can take an immediate 64-bit value.
Subtraction works in much the same way as addition, except it, well, subtracts. There is nothing to add here (no pun intended).
Actually, there is one thing. x86-64 also has the
cmp instruction, which is equivalent to sub
in every single way except one: instead of recording the result into the
destination register, sub simply discards it.
This is useful if you want to just compare the source to the destination -
flags will be updated as if a subtraction occurred (so you can deduce the
result of comparison from them), but the original value of the destination
operand will be preserved.
Both add and
sub set the overflow, zero, sign and carry
flags according to the result. The way overflow is detected is pretty
straightforward: if we're adding/subtracting two quantities with the
same sign bit, and the result has a different sign bit, the overflow flag must be
set. Otherwise, it must be cleared. Note that it is always assumed that the
result must have the same number of bits as the operands - thus adding two
8-bit integers can still overflow, even though values with larger bitness may
be technically representable on a given machine. Also, note that it's
impossible to get overflow by adding two numbers with different signs
(proving why that is true is left as an excercise to the reader ;)).
MUL and IMUL
Multiplication on x86 is kind of messy. One could think - it's just multiplication, how bad could it be? Well, we're about to see.
We'll start by examining the mul instruction,
which performs unsigned multiplication.
The thing you'll notice right away is that mul takes only one operand. That's because it implicitly assumes that the other operand is stored in one of:
al- for 8-bit multiplication;ax- for 16-bit multiplication;eax- for 32-bit multiplication;rax- for 64-bit multiplication.
mul tries to preserve data on
overflow. What this means is that the size of the result is twice that of the
operand. The result is written into two registers:
- For 8-bit multiplication, the upper half of the result goes into
ah, and the lower half goes intoal - For 16-bit multiplication, the upper half of the result goes into
dx, and the lower half goes intoax - For 32-bit multiplication, the upper half of the result goes into
edx, and the lower half goes intoeax - For 64-bit multiplication, the upper half of the result goes into
rdx, and the lower half goes intorax
In terms of flags, mul sets the overflow
and carry flags if the upper half of the result contains nonzero bits.
Otherwise, those flags are cleared. Just to keep us on our toes,
mul leaves the state of
zero and sign flags undefined, meaning they could either stay the same
or change arbitrarily after this instruction, regardless of the result.
Moving on, we have the signed multiplication instruction,
imul, which comes in three different flavors.
The first of them is the single-operand form. That one is basically equivalent
to mul, in every way, except it performs
signed multiplication. The difference between this form of
imul and mul
is best illustrated with the following example:
format PE64 NX GUI 6.0
entry start
section '.code' code readable executable
start:
xor rax, rax
int3
; when interpreted as unsigned 8-bit int:
; 0xfd is 253
; 0xfb is 251
; when interpreted as signed 8-bit int:
; 0xfd is -3
; 0xfb is -5
mov al, 0xfd
mov ah, 0xfb
mul ah
; after performing unsigned multiplication,
; ax will contain 0xf80f, which is
; 63503 (=253 * 251) in decimal. ah has the upper
; half, al has the lower half.
xor rax, rax
mov al, -3
mov ah, -5
imul ah
; after performing signed multiplication, ax
; will contain 0x000f which is 15 (= -5 * -3) in decimal.
ret
I recommend using a debugger to step through this example and see it for yourself.
The second variation of imul has two operands.
This time, it multiplies the source and the target operand, discards the
upper half of the intermediate result, and writes its lower half into the target
operand. The third variant of imul is similar,
except it takes three operands: it multiplies the last two and writes the result
into the first one. One limitation of the three-operand form of imul
is that the third operand has to be an immediate value.
For all variants of imul,
the carry and overflow flags are set if the value of the intermediate result
differs from the truncated result left-padded with its own sign bit, otherwise
both flags are cleared. Similarly to
mul, zero and sign flags become undefined.
An interesting side note: one curious thing you might notice if you look at what comes out of a C compiler is that compilers like to use signed multiplication to do arithmetic with unsigned numbers:

As the example above demonstrates, the compiler prefers to use signed multiply
in all cases except one, and even then, it might as well have been signed:
indeed, we can see that it does turn into a signed multiply when the call
to u8_u8u8 from main
gets inlined.
This behavior is explained by the fact that the results of signed and unsigned
multiplication are actually equivalent if you ignore the upper bits.
Since in C and C++ unsigned numbers are defined to wrap around on overflow,
ignoring those bits is legal, therefore it's perfectly fine to use two-operand
imul here (which is apparently more
convenient even for the soulless compiler). One caveat is that the same operands
may result in different values of the overflow flag between imul
and mul. For example, signed-multiplying 0xFFFC by 0xFFFD will
not set the overflow flag (it's just -3 * -5 in two's complement), but
unsigned-multiplying them would set the overflow flag. As far as the C
compiler is concerned, though, the C program that's being compiled has no way of
observing that difference.
DIV and IDIV
Unfortunately, integer division is also kind of awkward on x86. There are
two instructions for it - div and
idiv, which perform unsigned and signed
division respectively. Both assume the dividend to occupy 2x the number of bits
of the divisor. Also, both require the dividend to be stored in specific
register(s):
- If dividing by an 8-bit value, the dividend must be stored in ax;
- if dividing by a 32-bit value, the upper 32 bits of the dividend must be stored in dx, and the lower 32 bits must be stored in ax.
- if dividing by a 64-bit value, the upper 64 bits of the dividend go into rdx, and the lower 64 bits go into rax.
It's important to note that even if your dividend fully fits into the same number of bits as the divisor, you still need to populate the register corresponding to the upper half of the dividend - usually filling it with bits equal to your dividend's most significant bit. Allow mr. compiler to demonstrate:

What we can see here is the compiler first putting the dividend into eax,
then using a special instruction,
cdq to populate
edx with the necessary bits. cdq
sign-extends eax all the way into edx.
I'm pretty sure division was the only reason they added this group of instructions :-)
The divisor must be stored in either a register or memory, no division
by an immediate value is allowed. In other words, writing something like
div 7 isn't legal, you need to mov that 7 into
a register first.
Both the quotient and remainder are computed.
- If the divisor is 8-bit, the remainder goes into ah and the quotient goes into al;
- if the divisor is 16-bit, the remainder goes into dx and the quotient goes into ax;
- if the divisor is 32-bit, the remainder goes into edx and the quotient goes into eax;
- if the divisor is 64-bit, the remainder goes into rdx and the quotient goes into rax.
Note that if the quotient doesn't fit into its target register, a "division
error" exception is raised. For example, if you have 0xffff in ax,
and your div's operand is the bl register holding the
value 2, an exception will be raised because the result of that division can't
fit into al.
Finally, to complete the odd picture, all of the zero, sign, carry and overflow flags become undefined after executing a (signed or unsigned) division.
Logic Instructions
AND, OR, NOT, XOR
and, or
and xor function in pretty much the exact way
one would expect them to - given a source and a destination operand, they
perform the respective bitwise operation between the two, and write the result
to the destination operand. Similar to add,
both operands can't be memory.
They all clear the overflow and carry flags, and set the zero and sign flags according to the result.
The not instruction also does pretty much
what you'd expect (flip all the bits in the operand and write the result back),
and then, just to throw us a curveball, does not modify any flags at
all (i.e. mov al, x0ff followed by not al will not set the zero flag).
SHL, SAL, SHR and SAR
These four (or, I should say, three, because
sal and shl
are actually just different mnemonics for the same exact opcode) instructions
perform bit-shifts. If you know C, they do the same thing as operators <<
and >>.
Let's start with
shl/sal.
Like I said, these are just different mnemonics for the same exact instruction,
"shift left". It shifts the bit pattern of the destination operand (register or
memory) to the left by a given number of bits. I should add a clarification
here that "left" means the direction from the least significant bit towards
the most significant bit: 5 (0000 0101), if shifted left by 1 bit, would become
10 (0000 1010).
There are a couple of peculiarities about how this instruction works:
- The second operand (amount of bits to shift) is always an 8-bit integer;
- the second operand is either an immediate ("hardcoded") value, or the
clregister; - shifting left by N bits is functionally equivalent to shifting left by 1 bit, repeated N times;
- when shifting left by 1 bit, the carry flag is set to the value of the most significant bit before the shift.
These last two points essentially mean that bits are shifted out of the first operand through the carry flag. To illustrate with an example, if your first operand is 8 bits in size and contains the pattern 0100 0000, shifting left by 2 bits would set the carry flag to 1 - because the second most significant bit, which is 1, would get pushed out of the operand and into the carry flag.
The shr instruction does the same thing,
except it shifts the bit pattern to the right, and it's the least
significant bits that get shifted out through the carry flag. Otherwise, the
same notes as above apply.
The sar instruction is similar to
shr, except while
shr "shifts in" zeroes,
sar "shifts in" the sign bit
(most significant bit):
mov al, 0xF0 ; al = 1111 0000
shr al, 2 ; al = 0011 1100
mov al, 0xF0 ; al = 1111 0000
sar al, 2 ; al = 1111 1100
mov al, 0x0F ; al = 0000 1111
sar al, 2 ; al = 0000 0011
sar is mnemonic for Shift Arithmetic Right.
It should be noted that shifting the bit pattern left by 1 bit is equivalent to
multiplying by 2. Shifting it right is equivalent to dividing by 2, but if
you're working with signed numbers using two's complement, you need to preserve
the sign bit in order to maintain that property, which is exactly what
sar does.
Besides the effect on the carry flag (which has been discussed above), the shift instructions set the zero and sign flags according to the result. The value of the overflow flag is left undefined, unless the operation is a shift left by one bit. For left shift by 1 bit, the overflow flag is set if the most significant bit of the result is different from the carry flag and cleared otherwise.
Bonus Round: LEA
The lea instruction is technically not really
an ALU instruction - it's meant to compute the effective address of its second
operand (always memory) and store it in the first. However, you'll often see
see stuff like lea eax, [rdi + 64] when looking
at disassembly - even though rdi doesn't seem
to contain a pointer. This is because lea is
often used as a shortcut to "sneak in" plain old arithmetic operations,
especially since it allows to combine multiplication and addition into one step,
like so: lea rdx, [rbx*8 + 8].
lea does not modify any flags.
QBX Implementation
Now we'll take a look at how the arithmetic and logic instructions are implemented in the QBX virtual machine. One big difference is that our arithmetic instructions will only work with registers - no immediate values or memory. If you want to do arithmetic with a value, you will need to move it to a register first. This makes VM implementation a bit easier (and smaller) at the cost of it being more annoying to program for the VM.
As a reminder, most QBX instructions (except those that take an immediate value) are encoded with a single 16-bit opcode. Things like "add registers q0 and q1" and "add registers q2 and q1" are actually implemented as different opcodes. This is done in order to be able to map QBX registers directly onto x86-64 registers. We use a bit of assembler macro magic to spare ourselves the tedious task of implementing every single opcode manually.
With that in mind, let's take a look at the implementations of QBX arithmetic and logic instructions.
ADD and SUB
First, the code:
; addition instructions
rept QBX_NUM_REGISTERS sreg:0 {
rept QBX_NUM_REGISTERS dreg:0 \{
; byte-sized operands
insn addbq\#dreg\#q#sreg
add q\#dreg\#b, q#sreg#b
update_qbx_flags = 1
endinsn
; word-sized operands
insn addwq\#dreg\#q#sreg
add q\#dreg\#w, q#sreg#w
update_qbx_flags = 1
endinsn
\}
}
; subtraction instructions
rept QBX_NUM_REGISTERS sreg:0 {
rept QBX_NUM_REGISTERS dreg:0 \{
; byte-sized operands
insn subbq\#dreg\#q#sreg
sub q\#dreg\#b, q#sreg#b
update_qbx_flags = 1
endinsn
; word-sized operands
insn subwq\#dreg\#q#sreg
sub q\#dreg\#w, q#sreg#w
update_qbx_flags = 1
endinsn
\}
}
We've already seen the nested repts along with
the insn and
endinsn macros in the
previous post. The idea is to generate
add/sub instructions for every possible combination of registers, to handle
adding/subtracting both 16- and 8-bit values. The # sign is FASM's token
pasting operator (which is used to concatenate macro args to other tokens), and
the backslash thing is just something you have to do with nested macros.
The instructions themselves are implemented in a straightforward manner, by
invoking their x86-64 counterparts. However, there's one implementation detail
that bears further elaboration, namely the update_qbx_flags = 1
part.
When we execute x86-64 instructions that are meant to emulate QBX instructions,
we rely on the processor to update the flags state accordingly. We then immediately
save the state of the x86-64 flags register, and commit it to the QBX flags register.
That's the main purpose of the endinsn macro.
However, we can't simply override the QBX flags with the current state of x86-64
flags at the end of every instruction implementation. The problem is that there
are some QBX instructions which should not change any QBX flags, but their
implementation contains some instructions that do change the x86-64 flags.
You've already seen one such instruction, it's the "move immediate value to
register":
; move immediate byte-sized value into register.
rept QBX_NUM_REGISTERS reg:0 {
insn movibq#reg
mov q#reg#b, byte [qbx_mem + qip]
add qip, 1
endinsn
}
Since add actually changes x86-64 flags, if we
were to override the QBX flags at the end of this instruction, we'd corrupt our
VM's state. Therefore we employ a bit of conditional assembly and explicitly
mark instructions that do need to update flags -
that's what the update_qbx_flags = 1 part is
for. Also, we're extra careful to not let QBX flags get messed up before we've
had a chance to save them - basically, they need to be saved as soon as the
result of the virtual instruction has become available. Once they're saved, we
have free rein to do any VM book-keeping, and after all the prep for
executing the next instruction is done (which may change x86-64 flags
significantly), we set the state of the x86-64 flags register back to whatever
is in the QBX flags register. The next instruction implementation then sees
those flags as if nothing had occurred in between.
MUL and SMUL
We're taking some liberties with multiplication. QBX is going to have two
instructions for multiplication - mul and
smul, for performing unsigned and signed
multiplications respectively. However, we're going to be throwing away the upper
bits of the "extended" result - the size of the result of the multiplication will be
the same as the size of the operands. The only difference between the signed and
unsigned multiplication, then, is going to be the effect on the overflow flag.
Unlike x86-64, both multiplication instructions are going to have two
operands, both can be arbitrary registers. None of that implicit register stuff.
Let's look at the code:
; unsigned multiplication
rept QBX_NUM_REGISTERS sreg:0 {
rept QBX_NUM_REGISTERS dreg:0 \{
; byte-sized operands
insn mulbq\#dreg\#q#sreg
xor rax, rax
mov al, q\#dreg\#b
mul q#sreg#b
mov q\#dreg\#b, al
update_qbx_flags = 1
endinsn
; word-sized operands
insn mulwq\#dreg\#q#sreg
xor rax, rax
mov ax, q\#dreg\#w
mul q#sreg#w
mov q\#dreg\#w, ax
update_qbx_flags = 1
endinsn
\}
}
; signed multiplication
rept QBX_NUM_REGISTERS sreg:0 {
rept QBX_NUM_REGISTERS dreg:0 \{
; byte-sized operands
insn smulbq\#dreg\#q#sreg
xor rax, rax
mov al, q\#dreg\#b
imul q#sreg#b
mov q\#dreg\#b, al
update_qbx_flags = 1
endinsn
; word-sized operands
insn smulwq\#dreg\#q#sreg
imul q\#dreg\#w, q#sreg#w
update_qbx_flags = 1
endinsn
\}
}
Pretty self-explanatory stuff here. We use the two-operand form of imul to multiply word-sized operands. For the rest, we get the first operand into rax, multiply by the second,
then write the result into the first operand. We actually have to use the
single-operand version of imul for 8-bit operands
because the two- and three-operand versions don't have forms that take 8-bit registers,
unfortunately.
DIV and SDIV
We'll simplify division for QBX too. First of all, the dividend is always
16 bit in size, and is stored in the q0
register. It may be divided by either a 8 or 16-bit value stored in a register,
but either way the quotient is written to q0
and the remainder to q1.
div performs unsigned division, while
sdiv performs signed division. They have the
same effect on flags is their x86-64 counterparts.
; unsigned division
rept 3 sreg {
; byte-sized operands
insn divbq#sreg
xor dx, dx
xor ax, ax
mov ax, q0w
movzx cx, q#sreg#b
div cx
mov q0, ax
mov q1, dx
update_qbx_flags = 1
endinsn
; word-sized operands
insn divwq#sreg
xor rax, rax
xor rdx, rdx
mov ax, q0w
div q#sreg#w
mov q0, ax
mov q1, dx
update_qbx_flags = 1
endinsn
}
; signed division
rept 3 sreg {
; byte-sized operands
insn sdivbq#sreg
xor dx, dx
xor ax, ax
mov ax, q0w
movzx cx, q#sreg#b
idiv cx
mov q0, ax
mov q1, dx
update_qbx_flags = 1
endinsn
; word-sized operands
insn sdivwq#sreg
xor rax, rax
xor rdx, rdx
mov ax, q0w
idiv q#sreg#w
mov q0, ax
mov q1, dx
update_qbx_flags = 1
endinsn
}
Note that there's no need to have "divide by q0" because q0 holds the dividend.
Logic Instructions
Logic instruction implementations are all straightforward and kind of the
same, so I'm only going to show and here:
; bitwise and instructions
rept QBX_NUM_REGISTERS sreg:0 {
rept QBX_NUM_REGISTERS dreg:0 \{
; byte-sized operands
insn andbq\#dreg\#q#sreg
and q\#dreg\#b, q#sreg#b
update_qbx_flags = 1
endinsn
; word-sized operands
insn andwq\#dreg\#q#sreg
and q\#dreg\#w, q#sreg#w
update_qbx_flags = 1
endinsn
\}
}
You can see the rest in the QBX github repo, and that will be it for this post. In the next, and final, post, we will look at control flow instructions!
Like this post? Follow me on bluesky for more!